
Notice we had not found k previously because it was being multiplied by “b” which was zero. Now to make the last term equal to w 0 2 we need to find our remaining values, “d” and “k”. Doing this now gets rid of this second term by making it equal to zero. In this case, our "a" had already been set to 0 by the first term and to make this one zero we also have to set “b” to 0. We want to equal it to zero since we only want the w 0 2 to be left in the numerator. The second terms in the transfer function of equation 1 has the variables “a” and “b”. The first variable we want to get rid of is the first term, as 2. We see that the numerator that we want only has w 0 2 so we have to get rid of the other monomials to only leave w 0 2 by itself. Now we have to find the correct values for a,b,c, and d in equation 1 to end up with the transfer function of the low pass filter. The transfer function for a low pass Akerberg-Mossberg filter is seen below in equation 2.
With this transfer function, we can derive the transfer function for all types of filters like low pass, high pass, band pass, band stop, all pass, low pass notch and a high pass notch. We will only be manipulating these variables to change the numerator our denominator will stay the same. Now with this transfer function, we have 5 variables that we can play with to obtain our desired frequency response. General transfer function of the Akerberg-Mossberg with a summing circuit For the Ackerberg-Mossberg with a summing circuit the Transfer Function is the following equation below.Įquation 1. The summer adds the input signals and the signal from the band pass and low pass outputs.

The Akerberg-Mossberg Filter with a summing circuit added The summing circuit at the end of the Akerberg-Mossberg will look like this:įigure 4. The normalized version of the Akerberg-Mossberg Circuit above will need a summing configuration to be able to design a circuit and plot it on MATLAB. The advantages of using an Akerberg-Mossberg Filter is that the designing of it is easier and the Q (Quality Factor of the Frequency Response) is more predictable and the error in the gain is minimized. The Akerberg-Mossberg Filter as seen in Figure 3 is a Miller Integrator with a non-inverting integrator in the output. Frequency response of an Ideal Filter Akerberg-Mossberg Biquad Filter Unfortunately, these ideal filters cannot be made in real life, and we can only make filters that have a roll-off or slope as close to this as we can.įigure 2. An ideal perfect filter would have a slope of infinity. For every raise in order of a filter, there is a 6db/octave increase in the filter’s slope.

The order of a filter indicates how steep the slope is. The frequencies that we want to remove would be in the stop band when the magnitude is less than zero.ĭepending on which frequencies we want to remove, the location of the pass band will vary to create the main 4 filters types.
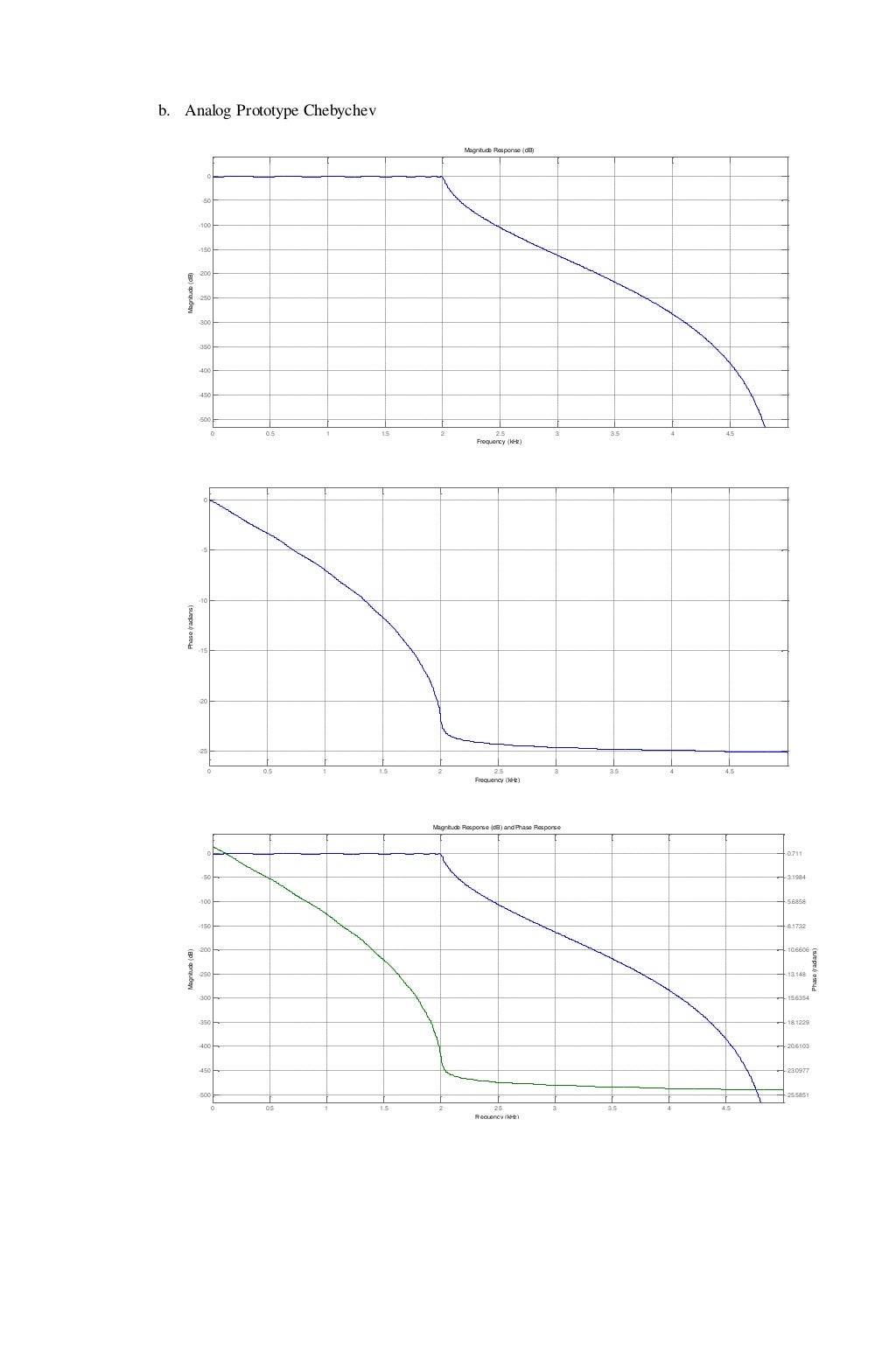
The frequencies after the cutoff frequencies f c are in the stop band. The frequencies in the pass band are the frequencies with an amplitude of 0 decibels or above. The above image is a bode plot for a low pass filter. The X-axis of the bode plot is the frequency of the filter.įigure 1. The magnitude or the amplitude is measured in decibels and plotted on the Y-axis of the Bode plot. It shows the magnitude of a signal with respect to the frequency. A Bode plot is a graph that tracks the response of frequencies. To understand the pass band and stop band in a filter, we need to understand Bode plots. It consists of two main bands: the pass band and the stop band. Filters can be used to remove noise from a system to make it cleaner. Introduction to FiltersĪ filter is a circuit that removes unwanted frequencies from a waveform. Become an Akerberg-Mossberg Filters champion.


 0 kommentar(er)
0 kommentar(er)
